K-近邻(k-NN)算法学习
k 近邻算法的基本概念,原理
基本概念
k 近邻算法是一种基本分类和回归方法。本篇文章只讨论分类问题的 k 近邻法。
基本原理
K 近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的 K 个实例,这 K 个实例的多数属于某个类,就把该输入实例分类到这个类中。(这就类似于现实生活中少数服从多数的思想)根据这个说法,咱们来看下引自维基百科上的一幅图:
如上图所示,有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所标示的数据则是待分类的数据。这也就是我们的目的,来了一个新的数据点,我要得到它的类别是什么?好的,下面我们根据 k 近邻的思想来给绿色圆点进行分类。
- 如果 K=3,绿色圆点的最邻近的 3 个点是 2 个红色小三角形和 1 个蓝色小正方形,少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。
- 如果 K=5,绿色圆点的最邻近的 5 个邻居是 2 个红色三角形和 3 个蓝色的正方形,还是少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。
从上面例子我们可以看出,k 近邻的算法思想非常的简单,也非常的容易理解,那么我们是不是就到此结束了,该算法的原理我们也已经懂了,也知道怎么给新来的点如何进行归类,只要找到离它最近的 k 个实例,哪个类别最多即可
KNN算法的优缺点
优点:精度高、对异常值不敏感、无数据输入假定
缺点:计算复杂度高、空间复杂度高(在高维情况下,会遇到「维数灾难」的问题)
k 近邻算法中 k 的选取以及特征归一化的重要性
选取 k 值以及它的影响
k 近邻的 k 值我们应该怎么选取呢?
如果我们选取较小的 k 值,那么就会意味着我们的整体模型会变得复杂,容易发生过拟合!恩~ 结论说完了,太抽象了吧你,不上图讲解号称通俗讲解的都是流氓~ 好吧,那我就上图来讲解
假设我们选取 k=1 这个极端情况,怎么就使得模型变得复杂,又容易过拟合了呢?
假设我们有训练数据和待分类点如下图: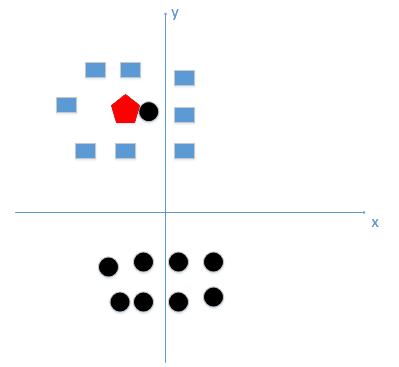
上图中有俩类,一个是黑色的圆点,一个是蓝色的长方形,现在我们的待分类点是红色的五边形。
好,根据我们的 k 近邻算法步骤来决定待分类点应该归为哪一类。我们由图中可以得到,很容易我们能够看出来五边形离黑色的圆点最近,k 又等于 1,那太好了,我们最终判定待分类点是黑色的圆点。
由这个处理过程我们很容易能够感觉出问题了,如果 k 太小了,比如等于 1,那么模型就太复杂了[1],我们很容易学习到噪声,也就非常容易判定为噪声类别,而在上图,如果,k 大一点,k 等于 8,把长方形都包括进来,我们很容易得到我们正确的分类应该是蓝色的长方形!如下图:
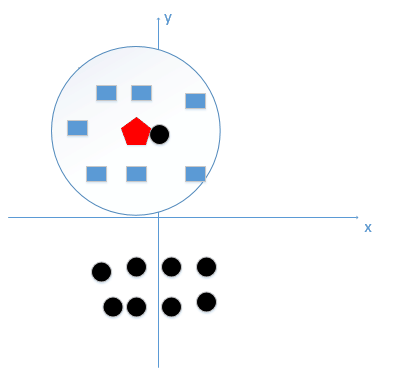
所谓的过拟合就是在训练集上准确率非常高,而在测试集上准确率低,经过上例,我们可以得到 k 太小会导致过拟合,很容易将一些噪声(如上图离五边形很近的黑色圆点)学习到模型中,而忽略了数据真实的分布!
如果我们选取较大的 k 值,就相当于用较大邻域中的训练数据进行预测,这时与输入实例较远的(不相似)训练实例也会对预测起作用,使预测发生错误,k 值的增大意味着整体模型变得简单。
我们想,如果 k = N(N 为训练样本的个数), 那么无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类。这时,模型是不是非常简单,这相当于你压根就没有训练模型呀!直接拿训练数据统计了一下各个数据的类别,找最大的而已!这好像下图所示:
我们统计了黑色圆形是 8 个,长方形个数是 7 个,那么哈哈,如果 k=N,我就得出结论了,红色五边形是属于黑色圆形的。
这个时候,模型过于简单,完全忽略训练数据实例中的大量有用信息,是不可取的。
恩,k 值既不能过大,也不能过小,在我举的这个例子中,我们 k 值的选择,在下图红色圆边界之间这个范围是最好的,如下图: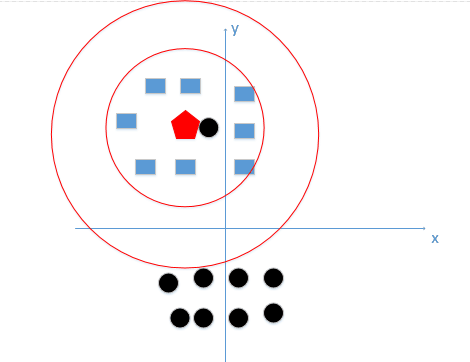
注:这里只是为了更好让大家理解,真实例子中不可能只有二维特征,但是原理是一样的,我们就是想找到较好的 k 值大小
那么我们一般怎么选取呢?李航博士书上讲到,我们一般选取一个较小的数值,通常采取 交叉验证法来选取最优的 k 值。(也就是说,选取 k 值很重要的关键是实验调参,类似于神经网络选取多少层这种,通过调整超参数来得到一个较好的结果)
距离的度量
在上文中说到,k 近邻算法是在训练数据集中找到与该实例最邻近的 K 个实例,这 K 个实例的多数属于某个类,我们就说预测点属于哪个类。
定义中所说的最邻近是如何度量呢?我们怎么知道谁跟测试点最邻近。这里就会引出我们几种度量俩个点之间距离的标准。
我们可以有以下几种度量方式:
设特征空间
这里
当
当
$$
L_{\infty}\left(x_{i}, x_{j}\right)=\max {l}\left|x{i}^{(l)}-x_{j}^{(l)}\right|
$$
其中当
特征归一化
首先举例如下,我用一个人身高(cm)与脚码(尺码)大小来作为特征值,类别为男性或者女性。我们现在如果有5个训练样本,分布如下:
A [(179,42),男] B [(178,43),男]
C [(165,36)女] D [(177,42),男]
E [(160,35),女]
通过上述训练样本,我们看出问题了吗?
很容易看到第一维身高特征是第二维脚码特征的4倍左右,那么在进行距离度量的时候,我们就会偏向于第一维特征。这样造成俩个特征并不是等价重要的,最终可能会导致距离计算错误,从而导致预测错误。口说无凭,举例如下:
现在我来了一个测试样本 F(167,43),让我们来预测他是男性还是女性,我们采取 k=3 来预测。
下面我们用欧式距离分别算出F离训练样本的欧式距离,然后选取最近的 3 个,多数类别就是我们最终的结果,计算如下:
由计算可以得到,最近的前三个分别是 C,D,E 三个样本,那么由 C,E 为女性,D 为男性,女性多于男性得到我们要预测的结果为女性。
这样问题就来了,一个女性的脚 43 码的可能性,远远小于男性脚 43 码的可能性,那么为什么算法还是会预测 F 为女性呢?那是因为由于各个特征量纲的不同,在这里导致了身高的重要性已经远远大于脚码了,这是不客观的。所以我们应该让每个特征都是同等重要的!这也是我们要归一化的原因!归一化公式如下:
一般来说,假设进行 kNN 分类使用的样本特征为${(x_{i1},x_{i2},...,x_{in}) }{i=1}^m
M{j}=\max {i=1, \ldots, m} x{i j}-\min {i=1, \ldots, m} x{i j}
d\left(\left(y_{1}, \ldots, y_{n}\right),\left(z_{1}, \ldots, z_{n}\right)\right)=\sqrt{\sum_{j=1}^{n}\left(\frac{y_{j}}{M_{j}}-\frac{z_{j}}{M_{j}}\right)^{2}}
$$
文章大部分内容转载自忆臻的一文搞懂 k 近邻(k-NN)算法
